Learning Center
Introduction to Probability
Probability is a field of mathematics that deals with calculating the likelihood of occurrence of a specific event.
The likelihood of an event is expressed as a number between zero (the event will never occur) and one (the event is certain). For example, the probability of an outcome of heads on the toss of a fair coin is ½ or 0.5. The probability of an event can also be expressed as a percentage (e.g., an outcome of heads on the toss of a fair coin is 50% likely) or as odds (e.g., the odds of heads on the toss of a fair coin is 1:1).
A single toss of a coin is an event (also called a trial) that is not connected to or influenced by other events. When a coin is tossed twice, the coin has no memory of whether it came up heads or tails the first time, so the second toss of the coin is independent. The probability of heads on the first toss is 50%, just as it is on all subsequent tosses of the coin.
The two outcomes of the toss of a coin are heads or tails. For any individual toss of the coin, the outcome will be either heads or tails. The two outcomes (heads or tails) are therefore mututally exclusive; if the coin comes up heads on a single toss, it cannot come up tails on the same toss.
There are two useful rules for calculating the probability of events more complicated than a single coin toss.
The first is the Product Rule. This states that the probability of the occurrence of two independent events is the product of their individual probabilities. The probability of getting two heads on two coin tosses is 0.5 x 0.5 or 0.25.
The Product Rule is evident from the visual representation of all possible outcomes of tossing two coins shown above. The probability of getting heads on the toss of a coin is 0.5. If we consider all possible outcomes of the toss of two coins as shown, there is only one outcome of the four in which both coins have come up heads, so the probability of getting heads on both coins is 0.25.
The second useful rule is the Sum Rule. This states that the probability of the occurrence of two mutually exclusive events is the sum of their individual probabilities. As you can see from the picture, the probability of getting one head and one tail on the toss of two coins is 0.5. There are two different ways that this can happen. The first coin can come up heads and the second coin can come up tails, or the first coin can come up tails and the second coin can come up heads. In any single trial, it is not possible for both of these outcomes to occur, so these are mutually exclusive.
There are four possible mutually exclusive outcomes on the toss of two coins as shown, each with a probability of 0.25. The sum of the probability of two of these outcomes (heads, tails or tails, heads) is 0.25 + 0.25 or 0.5.
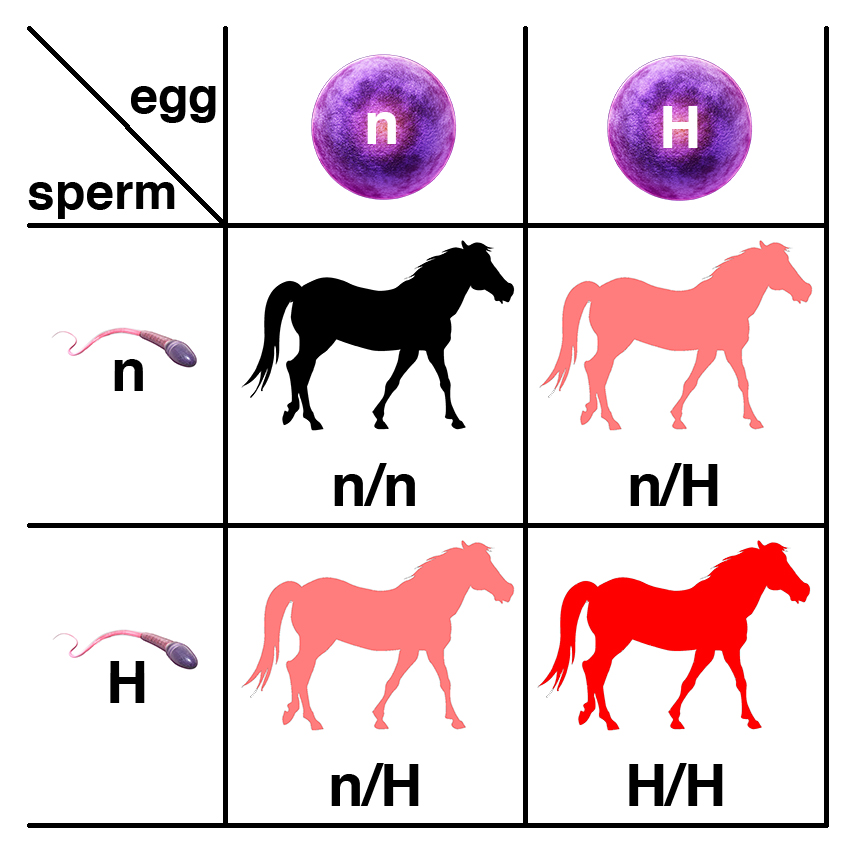
The basic rules of probability apply to horse breeding as well. Horses have two copies of each of their genes. A horse that is heterozygous for the mutation that causes HYPP has the genotype n/H. When this horse makes gametes (sperm or egg), there is only one copy of each gene in the gamete. There is a 50% chance that a gamete has the n allele and a 50% chance that a gamete has the H allele.
The process of fertilization is like the toss of two coins. If a stallion that is n/H is bred to a mare that is n/H, the chance that the foal will be n/n is 0.25, while the chance that the foal will be n/H is 0.5. The Sum Rule and the Product Rule apply to horse breeding in the same way that they apply to coin tosses.
EquiSeq is a biotech company offering
genetic testing for horses.
Resources
© 2017 – 2023 EquiSeq Inc. All rights reserved.